Search Advanced Algorithmic Design
Instructors: Mark Collins (mark@proxyarch.com) Toru Hasegawa (toru@proxyarch.com)
 
 
Many properties of objects are invariant under transformations - for instance a box is still the same height and has the same volume regardless of whether it is translated or rotated. Matrix transformations are a way to describe the movement and orientation of an object seperate from its geometric description. They are used extensively in graphics software, from FX packages like Maya to 3D games. They are also used in Processing - we will approach the subject from a practical point of view so that the utility of these powerful commands can be unlocked for the casual programmer.
 
Example of two transformations applied to an object, where order of operations is key to its actual appearance.
 
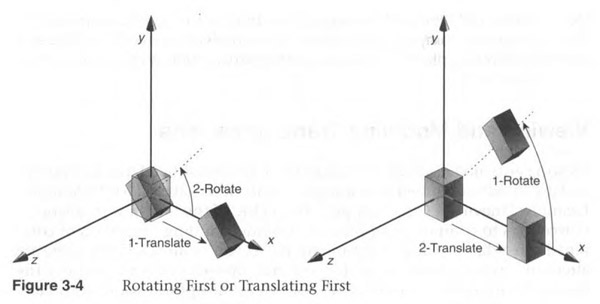
What is a matrix? A matrix is a conveniant way of storing transformation, more particularly scale, rotation, translation. Most software, including Processing, store this information in a 4x4 matrix. Matrixes allow you to multiply a 3D point, or vertex, by the matrix - the resulting 3D point is the "transformed" vertex. If the matrix describes a translation, the point will be translated by the amount specified. In Processing, we dont need to understand the mathematics of this, but it is important to understand how matrixes transform objects so that we properly order our operations (see the above diagram for the somewhat counter-intuitive way that transformations build on each other).

 

Link to Processing Applet here.
Commands used: PVector(), normalize(), rotate(), scale(), translate(), pushMatrix(), popMatrix()
 
This simple example shows both rotation and translation. It extensively uses the PVector object. Note that when we draw objects, we are always drawing them at {0,0} (the origin) - the fact that objects appear in different places and at different orientations are dependent on the transformations that we call *before* we make them..

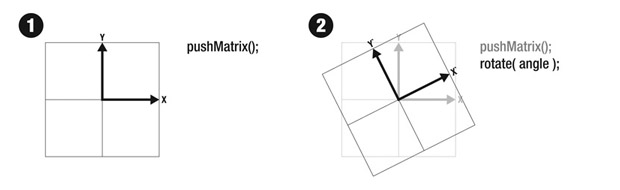
The most fundamental concept to understand about transformations in Processing is that the space in which objects are constructed is what is actuall transformed, not the object itself. This could be analagous to construction planes in Rhino - we are always drawing objects within a space. By defining a new origin for that space, or rotating the construction plane, new objects would appear to be translated and rotated. Objects drawn before these changes would be unaffected.

Consider the sequence below. We start by calling pushMatrix() - this saves the current matrix. Later, we will use popMatrix() to restore back to this state - effectively wiping any transformations in between. This is important since we sometimes want to draw several objects, each of which needs a custom transformation. We need to be able to get back to a default state. In the example below, we also call rotate() - in 2D, this rotates our coordinate space. Note that the space itself is now rotated.
 

If we now draw a simple line in our scene, it will inherit the rotation of the construction plane. Note that we are simply drawing a line straight up (the line starts at 0,0 and ends at 0,length - i.e. it does not have any horizontal component). The resulting line is rotated in our display, exactly the same amount that we specified in the rotate() command. Step 4 goes translates the space forward. Note that the orgin of our construction space {0,0} is now at the furthest point on the line we drew. Drawing an object, such as an ellipse, at {0,0} would place it at the tip of our line.
 

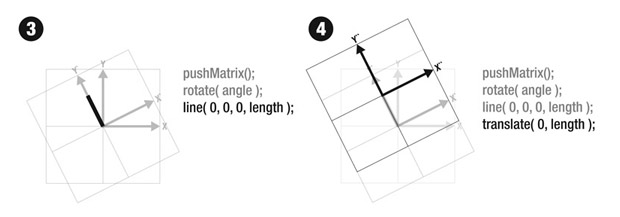
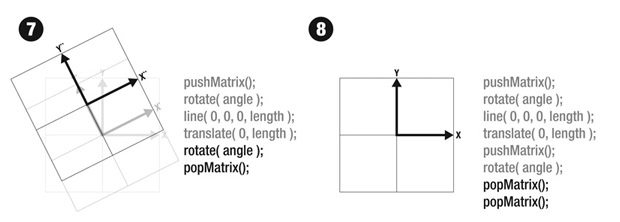
Matrixes that describe transformations can be be continually saved and restored - this is a function of the "matrix stack" that Processing manages. Anytime we want to save a transformation "state", we simply call pushMatrix() and it "pushes" it onto the matrix stack. We can then go back to this state by calling popMatrix(). This assumes that there will be an equal number of calls to pushMatrix() and popMatrix()..
 
 
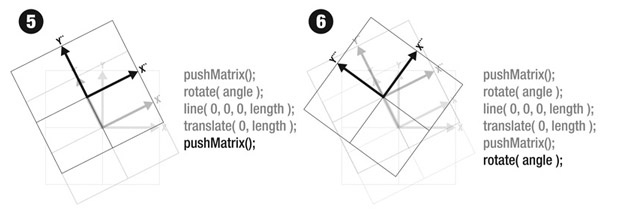
Below we show the effect of calling popMatrix() - by Step 8 we have returned to our original coordinate state. The first call to popMatrix() returns us back to the last call to pushMatrix(). The second call returns us to the default state that was created by the first call to pushMatrix(). Drawing an object at {0,0} would now put the object at the absolute origin.
 
 

Link to Processing Applet here.
Commands used: rotate(), scale(), translate(), pushMatrix(), popMatrix()
 
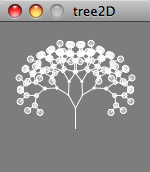
This example shows transformations being called within a recursive function. Recursion will be covered in Class #2. Rotations and translations create the branches, and recursive calls to pushMatrix() and popMatrix() allows for each branch to inherit transformations of parent branches.